题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
在10.5.7节曾提到z变换的卷积性质,为了证明这个性质成立,现从卷积和表示式入手,即(a)将式(P10.
在10.5.7节曾提到z变换的卷积性质,为了证明这个性质成立,现从卷积和表示式入手,即
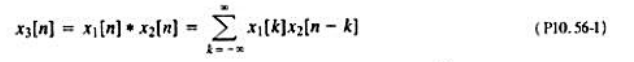
(a)将式(P10.56.1)取z变换,并利用式(10)证明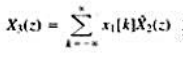 其中
其中 (z)是x2[n—k]的z变换
(z)是x2[n—k]的z变换
(b)利用(a)的结果和表10.1中的性质15.2,证明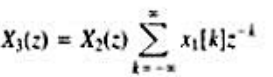
(c)由(b),证明X3(z)=X1(z)X2(2)这是式(10.81)所陈述的。
 如搜索结果不匹配,请 联系老师 获取答案
如搜索结果不匹配,请 联系老师 获取答案


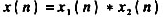 ,若要直接把相互卷积的信号x1(n)与x2(n)分开将遇到困难.但是,对于两个相加的信号往往容易借助某种线性滤波方法使二者分离.图8-5示出用同态滤波解卷积的原理框图,其中各部分作用如下:
,若要直接把相互卷积的信号x1(n)与x2(n)分开将遇到困难.但是,对于两个相加的信号往往容易借助某种线性滤波方法使二者分离.图8-5示出用同态滤波解卷积的原理框图,其中各部分作用如下: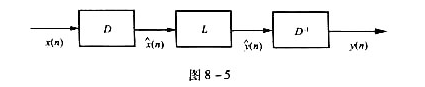
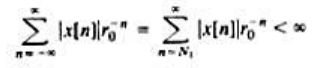
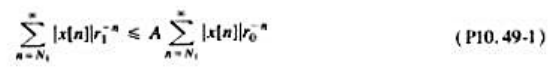
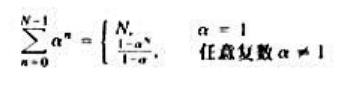
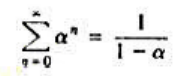
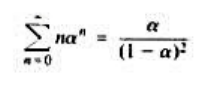
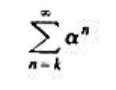
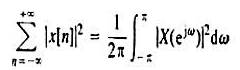
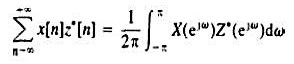
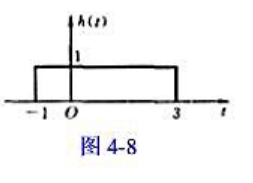
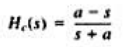 其中a为正实数。证明H.(jw)=1
其中a为正实数。证明H.(jw)=1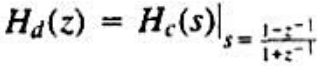 证明:Hd(z)有一个极点(在单位圆里)和一个零点(在单位圆外).
证明:Hd(z)有一个极点(在单位圆里)和一个零点(在单位圆外).